Chapter 6.2. Nested Loops – Exam Problems
In the previous chapter, we introduced nested loops and how to use them for drawing various kinds of figures on the console. We've learned how to print figures with different sizes, establishing suitable logic construction by using single and nested for loops in combination with different calculations and program logic:
for r in range(5):
print("*", end="")
for c in range(5):
print(" *", end="")
print("")
We also learned the operator *, which lets you for defined by us a number of times, a given string to be printed:
print_me = ('abc' * 2)
Exam Problems
Now let's solve some Exam Problems to consolidate what we have learned and to develop our algorithmic thinking.
Problem: Draw Fort
Write a program, that reads from the console an integer n and draws a fortress with a width of 2 * n columns and height of n rows, as in the below-given examples. The left and the right inner columns have a width of n / 2.
Input Data
The program input consists one element (argument) - integer n within the range [3 … 1000].
Output Data
Print on the console n text lines, depicting the fortress, just as in the examples below.
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 3 | /^\/^\| |\_/\_/ |
4 | /^^\/^^\| || |\__/\__/ |
| Input | Output | Input | Output |
|---|---|---|---|
| 5 | /^^\__/^^\| || || __ |\__/ \__/ |
8 | /^^^^\____/^^^^\| || || || || || ____ |\____/ \____/ |
Hints and Guidelines
By the set task condition, we can see that the input data will contain only one integer within the range [3 … 1000]. Therefore, we will convert the input value into int type:
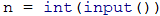
After we've declared and initialized the input data, we have to divide the fortress into three parts:
- roof
- body
- base
We can see from the examples, that the roof consists of two towers and a middle part. Each tower has a beginning /, middle part ^ and an end \.
By the set task condition the left and the right inner columns have a width of n / 2, therefore we can save this value as a separate variable, keeping in mind, that if we receive an odd number as input, the result of dividing by two will be a number with a whole and fractional part. In this case, we need only the whole part (in the set task condition we can see, that when the input is equal to 3 the count of ^ in the inner part column is equal to 1, and the input of 5 it is 3), we can separate it with the function math.trunc(…) and to save only its value in our new variable:
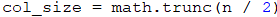
| It's always a good practice, whenever we have an expression with the value we intend to use more than once, to keep it in a variable. In this way, on the one hand, our code will be easier to read, and on the other hand, it will be easier to correct possible errors, as we will not have to look for each use of the expression separately. |
We also declare a second variable, which will keep the value of the part between the two towers. By the set task condition, we know that the total width of the fortress is n * 2. In addition, we have two towers with one slash for a start and one slash for an end (a total of 4 characters), and width of col_size. Therefore, to get the number of characters in the middle part, we have to subtract the size of the towers from the width of the entire fortress: 2 * n - 2 * col_size - 4.

To print the roof part, on the console we will use the format(…) method in combination with the operator *, which joins a given string n number of times:
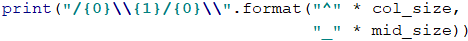
\ is a special symbol in Python and using it solely in the method print(…), the console will not print it out, so with \\ we indicate on the console, that we want to print out exactly this character, without interpreting it as a special character (character escaping it). |
The fortress body consists of beginning |, middle part (white spaces), and an end |. The middle part of white spaces has a width of 2 * n - 2. The number of rows for the walls can be determined from the given examples: n - 3:

To draw a penultimate row, which is part of the base, we need to print a beginning |, middle part (white space)_(white space), and an end |. To do this, we can use already declared variables col_size and mid_size because as we see from the examples they are equal to the number of _ in the roof:

We add to the value of white spaces + 1 because in the examples we have one white space more.
The structure of the fortress base is the same as the one in the roof. It includes two towers and a middle part. Each tower begins with \, followed by a middle part _, and an end /.

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/1056#0.
Problem: Butterfly
Write a program, that takes an integer n from the console and draws butterfly with a width of 2 * n - 1 columns and height of 2 * (n - 2) + 1 rows as in the examples below. The left and the right part have a width of n - 1.
Input Data
The input consists of one element (argument) - integer n in the range [3 … 1000].
Output Data
Print on the console 2 * (n - 2) + 1 text rows, representing the butterfly, exactly as shown in the examples.
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 3 | *\ /* @ */ \* |
5 | ***\ /***---\ /---***\ /*** @ ***/ \***---/ \---***/ \*** |
| Input | Output |
|---|---|
| 7 | *****\ /*****-----\ /-----*****\ /*****-----\ /-----*****\ /***** @ *****/ \*****-----/ \-----*****/ \*****-----/ \-----*****/ \***** |
Hints and Guidelines
Similar to the previous task, we can see from the condition, that the input data will consist of only one integer in the range [3 … 1000]. That's why we will convert the input value into int type:

We can divide the figure into 3 parts - upper wing, body, and lower wing. To draw the upper wing of the butterfly, we have to divide it into three parts - a beginning with *, a middle part with \ /, and an end with *. After looking at the examples, we can say that the upper wing of the butterfly is with a size of n - 2:

To draw the upper wing we make a loop repeated half_row_size number of times:
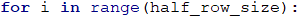
We can see in the examples, that on an even row we have a beginning *, middle part \ / and an end *, on the other hand on an odd row we have a beginning -, middle part \ / and an end -. Therefore, at each iteration of the loop, we have to do an if-else check to see whether the row that we print is even or odd. From the examples given in the set condition, we can see that the number of star characters and dashes on each row is equal to n - 2, i. e. we can use again the variable half_row_size to print them:

To draw the butterfly body, we have to print exactly one row on the console. The structure of the body has a beginning (white space), middle part @, and an end (white space). From the examples we can see, that the number of the white spaces is equal to n-1:
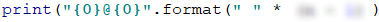
What is left now is to print on the console the lower wing, which is analogical to the upper wing: we only need to swap the places of the slashes.
Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/1056#1.
Problem: Stop
Write a program, that takes an integer n from the console and draws a STOP warning sign with size as shown in the examples below.
Input Data
The input consists of one element (argument) - integer n in the range [3 … 1000].
Output Data
Print on the console text lines, representing the STOP warning sign, just as in the examples.
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 3 | ...._______.......//_____\\.....//_______\\...//_________\\.//___STOP!___\\\\___________//.\\_________//...\\_______//.. |
6 | ......._____________.............//___________\\...........//_____________\\.........//_______________\\.......//_________________\\.....//___________________\\...//_____________________\\.//_________STOP!_________\\\\_______________________//.\\_____________________//...\\___________________//.....\\_________________//.......\\_______________//.........\\\___________//..... |
| Input | Output |
|---|---|
| 7 | ........_______________...............//_____________\\.............//_______________\\...........//_________________\\.........//___________________\\.......//_____________________\\.....//_______________________\\...//_________________________\\.//___________STOP!___________\\\\___________________________//.\\_________________________//...\\_______________________//.....\\_____________________//.......\\___________________//.........\\_________________//...........\\_______________//...... |
Hints and Guidelines
As in the previous examples, the input data will be on one line, which will contain one int in the range [3 … 1000]:

We can divide the figure into 3 parts - upper, middle, and lower. The upper part consists of two subparts - a starting line and lines in which the sign widens. The starting line consists of beginning ., middle part _ and an end .. After looking at the examples, we can see that the beginning has a size of n + 1 and it's better to keep this value as a separate variable. We also have to create a second variable, in which we will keep the value of the first-row middle part which has a size of 2 * n + 1:
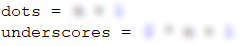
Once we have declared and initialized the two variables, we can print the first row on the console:

To draw the rows in which the sign is getting "wider", we have to create a loop, that iterates n number of times. The row structure consists of a beginning ., // + middle part _ + \\ and an end .. To reuse the already created variables, we have to decrease dots by 1 and underscores by 2, because we've already printed the first row, and the dots and underscores in the top part of the figure are decreasing on each row:
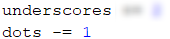
At each subsequent iteration the beginning and the end decrease by 1, and the middle part increases by 2:

The middle part of the figure begins with // + _, middle part STOP! and an end _ + \\. The count of the underscores _ is (underscores - 5) / 2:

The lower part of the figure, in which the width of the sign decreases, can be done by creating a loop, that iterates n number of times. The structure of a row should have a beginning . + \\, middle part _ and an end // + .. The number of the dots in the first loop iteration has to be 0 and each subsequent has to increase by one. Therefore we can say that the dots in the lower part of the figure are equal to i. To ensure proper operation of our program, on each loop iteration, we have to decrease the number of _ by 2:

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/1056#2.
Problem: Arrow
Write a program that receives from the console an odd integer n and draws a vertical arrow with size as in the examples below.
Input Data
The input is an odd integer n (argument) within the range [3 … 79].
Output Data
Print on the console a vertical arrow, in which "#" (hash sign) marks the outline of the arrow, and "." - the rest.
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 3 | .###..#.#.##.##.#.#...#.. |
5 | ..#####....#...#....#...#....#...#..###...###.#.....#...#...#.....#.#.......#.... |
| Input | Output |
|---|---|
| 9 | ....#########........#.......#........#.......#........#.......#........#.......#........#.......#........#.......#........#.......#....#####.......#####.#.............#...#...........#.....#.........#.......#.......#.........#.....#...........#...#.............#.#...............#........ |
Hints and Guidelines
From the explanation we see that the input data will be read from one input line only, which will contain an integer within the range [3 … 1000]. That's why we will convert the input value into int type:

We can divide the figure into 3 parts - upper, middle, and lower. The upper part consists of two subparts - the first row and the body of the arrow. We can see from the examples, that the count of the outer dots in the first row and the body of the arrow are equal to (n - 1) / 2. We can keep this value in a variable outer_dots:
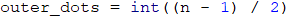
The count of the inner dots in the body of the arrow is equal to (n - 2). We have to create the variable inner_dots, which will keep this value:
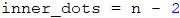
We can see from the examples the structure of the first row. We can use the declared and initialize by us variables outer_dots and n, to print the first row:

To draw the body of the arrow, we have to create a loop, which iterates n - 2 number of times:

The middle part of the figure is made of a beginning #, middle part . and an end #. The count of # is equal to outer_dots and that is why we will use the same variable:

To draw the lower part of the arrow, we have to assign new values of the two variables outer_dots and inner_dots.
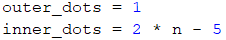
On each loop iteration outer_dots increase by 1, and inner_dots decrease by 2. We can notice, that on the penultimate row the inner_dots value will be 1 and on each subsequent loop iteration will be a negative number. Since the operator * cannot concatenate symbol 0 or a negative number of times in a string, it will print nothing on the console. To avoid that we can print the last row of the figure separately. The height of the lower part of the arrow is n - 1, therefore the loop, that will print all the rows, except the last one, have to iterate n - 2 number of times:

The last row of our figure is made of a beginning ., middle part # and an end .. The count of . is equal to outer_dots:
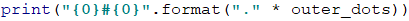
Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/1056#3.
Problem: Axe
Write a program, that receives an integer n and draws an axe with size as in the example below. The width of the axe is 5 * n columns.
Input Data
The input consists one element (argument) - integer n within range [2..42].
Output Data
Print on the console axe, as in the examples.
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 2 | ------**--------*-*-*******-*-------***- |
5 | ---------------**-----------------------*-*----------------------*--*---------------------*---*--------------------*----*----****************----*----****************----*-------------------*----*------------------********--- |
| Input | Output |
|---|---|
| 8 | ------------------------**--------------------------------------*-*-------------------------------------*--*------------------------------------*---*-----------------------------------*----*----------------------------------*-----*---------------------------------*------*--------------------------------*-------*-------*************************-------*-------*************************-------*-------*************************-------*-------*************************-------*-------------------------------*-------*------------------------------*---------*----------------------------*-----------*--------------------------***************---- |
Hints and Guidelines
From the explanation we see that the input data will be read from one input line only, which will contain an integer within the range [2 … 42]. That's why we will use int type. After that, for the solution we need to calculate the dashes in the left, the dashes in the middle, the dashes in the right, and the whole figure length:

Once we have declared and initialized the variables, we can draw the figure, starting with the upper part. We can see from the examples what the structure of the first row is and we can create a loop that iterates n number of times. At each loop iteration, the middle dashes are increasing by 1, and the right dashes are decreasing by 1:
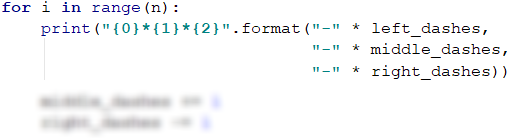
Now we have to draw the handle of the axe. To be able to use the newly created variables, when drawing the handle of the axe, we have to decrease the middle dashes by 1 and increase these on the right and left by 1.
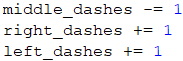
The handle of the axe we can draw, by iterating a loop that repeats n / 2 number of times. We can set this value into a separate variable, considering that when dividing odd number inputs by 2 the result will be a real number with a whole and fractional part. Since in this case, we need only the whole part (from the example condition we see that at input 5 the height of the axe handle is 2), we can use the math.trunc(…) method, to save only its value in our new variable axe_height. We get the structure of the handle from the examples given:

The lower part of the figure should be divided into two subparts - the head of the axe and the last row of the figure. We will print on the console the head of the axe, by making a self iterating loop axe_height - 1 number of times. On each iteration, the left dashes and the right dashes decrease by 1, and the middle dashes increase by 2:

For the last row of the figure, we can use again, the already declared variables left_dashes, middle_dashes, right_dashes.

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/1056#4.